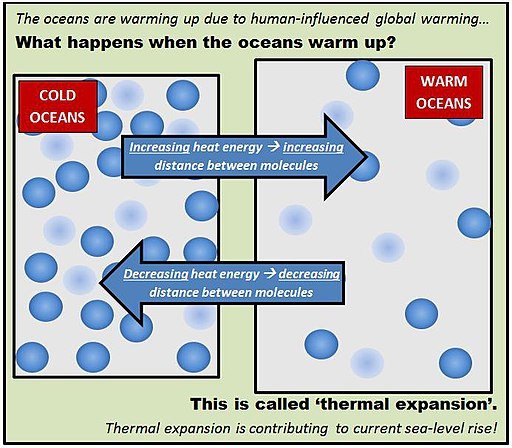
Thermal Dilation is the variation that occurs in the dimensions of a body when subjected to a temperature variation.
In general, bodies, be they solid, liquid or gaseous, increase in size as their temperature increases.
Table of Contents
Thermal Dilation of Solids
An increase in temperature causes increased vibration and distancing between the atoms that make up a solid body. As a consequence, there is an increase in its dimensions.
Depending on the most significant expansion in a given dimension (length, width and depth), the solids dilation is classified as linear, superficial and volumetric.
Linear dilation
Linear dilatation takes into account the dilatation suffered by a body in only one of its dimensions. This is the case, for example, with a thread, where its length is more relevant than its thickness,
To calculate linear expansion we use the following formula:
?L = L 0 .?.??
At where,
?L : Variation of length (m or cm)
L 0 : Initial length (m or cm)
? : Coefficient of linear expansion (ºC -1 )
?? : Temperature variation (ºC)
Surface Expansion
The superficial dilation takes into account the dilation of a given surface. This is the case, for example, with a thin metal plate.
To calculate the superficial dilatation we use the following formula:
?A = A 0 .?.??
At where,
?A : Variation of the area (m 2 or cm 2 )
A 0 : Initial area (m 2 or cm 2 )
? : Coefficient of surface expansion (ºC -1 )
?? : Temperature variation (ºC)
It should be noted that the coefficient of surface expansion (?) is equal to twice the value of the coefficient of linear expansion (?), that is:
? = 2. ?
Volumetric Dilation
The volumetric dilatation results from the increase in the volume of a body, which happens, for example, with a gold bar.
To calculate the volumetric expansion we use the following formula:
?V = V 0 .?.??
At where,
?V : Variation of volume (m 3 or cm 3 )
V 0 : Initial volume (m 3 or cm 3 )
? : Volumetric expansion coefficient (ºC -1 )
?? : Temperature variation (ºC)
Note that the volumetric expansion coefficient ( ?) is three times greater than the coefficient of linear expansion (?), ie:
? = 3. ?
Linear Dilation Coefficients
The dilation suffered by a body depends on the material that composes it. In this way, in the calculation of the dilation, the substance of the material is taken into account by means of the coefficient of linear expansion (?).
The table below shows the different values ??that can be assumed by the coefficient of linear expansion for some substances:
| Substance | Coefficient of Linear Dilation (ºC -1 ) |
|---|---|
| Porcelain | 3.10 -6 |
| Common Glass | 8.10 -6 |
| Platinum | 9.10 -6 |
| Steel | 11.10 -6 |
| Concrete | 12.10 -6 |
| Iron | 12.10 -6 |
| Gold | 15.10 -6 |
| Copper | 17.10 -6 |
| Silver | 19.10 -6 |
| Aluminum | 22.10 -6 |
| Zinc | 26.10 -6 |
| Lead | 27.10 -6 |
Thermal Dilation of Liquids
Liquids, with some exceptions, increase in volume when their temperature increases, in the same way as solids.
However, we must remember that liquids do not have their own form, acquiring the shape of the container that contains them.
Therefore, for liquids, it makes no sense to calculate either linear or superficial dilatation, only the volumetric one.
In this way, we present below the table of the coefficient of volumetric expansion of some substances.
| Liquids | Coefficients of Volumetric Dilation (ºC -1 ) |
|---|---|
| Water | 1.3.10 -4 |
| Mercury | 1.8.10 -4 |
| Glycerin | 4.9.10 -4 |
| Alcohol | 11.2.10 -4 |
| Acetone | 14.93.10 -4 |
Exercises
Question: 1. A steel wire has a length of 20 m when its temperature is 40 ° C. What will be its length when its temperature is equal to 100 ºC? Consider the linear coefficient of expansion of the steel equal to 11.10 -6 ° C -1
Answer:
To find the final length of the wire, we first calculate its variation for this temperature variation. To do this, simply replace in the formula:
?L = L 0 .?.??
?L = 20:11:10 -6 . (100-40)
?L = 20:11:10 -6 (60) .
?L = 20.11.60.10 -6
?L = 13200.10 -6
?L = 0.0132
To know the final size of the steel wire, we have to add the initial length with the variation found:
L = L0 + ?L
L = 20 + 0.0132
L = 20.0132 m
Question: 2. A square aluminum plate has sides equal to 3 m when its temperature is equal to 80 ° C. What will be the variation of your area if the plate is subjected to a temperature of 100 ° C? Consider the linear expansion coefficient of aluminum 22.10 -6 ° C -1 .
Answer:
As the plate is square, to find the measurement of the initial area we must do:
A 0 = 3.3 = 9 m 2
The coefficient of linear expansion of aluminum was reported, however, to calculate the surface variation we need the value of ?. So, first let’s calculate this value:
? = 2. 22.10 -6 ° C -1 = 44.10 -6 ° C
We can now calculate the variation of the sheet area by replacing the values ??in the formula:
?A = A 0 .?.??
?A = 9.44.10 -6 . (100-80)
?A = 9.44.10 -6 . (20)
?A = 7920.10 -6
?A = 0.00792 m 2
The Area variation is 0.00792 m 2
Question: 3) A 250 ml glass vial contains 240 ml of alcohol at a temperature of 40 ° C. At what temperature will the alcohol begin to overflow from the bottle? Consider the linear coefficient of expansion of glass equal to 8.10 -6 ºC -1 and the alcohol volumetric coefficient 11.2.10 -4 ºC -1 .
Answer:
First we need to calculate the volumetric coefficient of the glass, since only its linear coefficient has been reported. Thus, we have:
? Glass = 3. 8. 10 -6 = 24. 10 -6 ° C -1
Both the bottle and alcohol will dilate and the alcohol will begin to overflow when its volume is greater than the volume of the bottle.
When the two volumes are equal, the alcohol will be on the verge of overflowing from the bottle. In this situation we have that the volume of alcohol is equal to the volume of the glass vial, ie V glass = V alcohol .
The final volume is found by making V = V 0 + ?V. Substituting in the expression above, we have:
V 0 glass + ?V glass = V 0 alcohol + ?V alcohol
Replacing the problem values:
250 + (250. 24. 10 -6 . ??) + = 240 (240. 11,2. 10 -4 . ??)
250 + (0.006. ??) = 240 + (0.2688. ??)
0.2688. ?? – 0.006. ?? = 250 – 240
0.2628. ?? = 10
?? = 38 ° C
To know the final temperature, we have to add the initial temperature with its variation:
T = T 0 + ?T
T = 40 + 38
T = 78 ° C